朴素 Dijkstra 算法

时间复杂度

  • $O(n^2)$

算法应用情景：

  • 不含有负权边的图中

整体思路：

  • 初始化，将起点加入已更新的点中，并将起点的 dist 设为 0，其余点的 dist 为 INF，代表没更新
  • 循环 n - 1 次，每次更新一个点，
  • 用这个点更新其他点到起点的距离

如图所示：

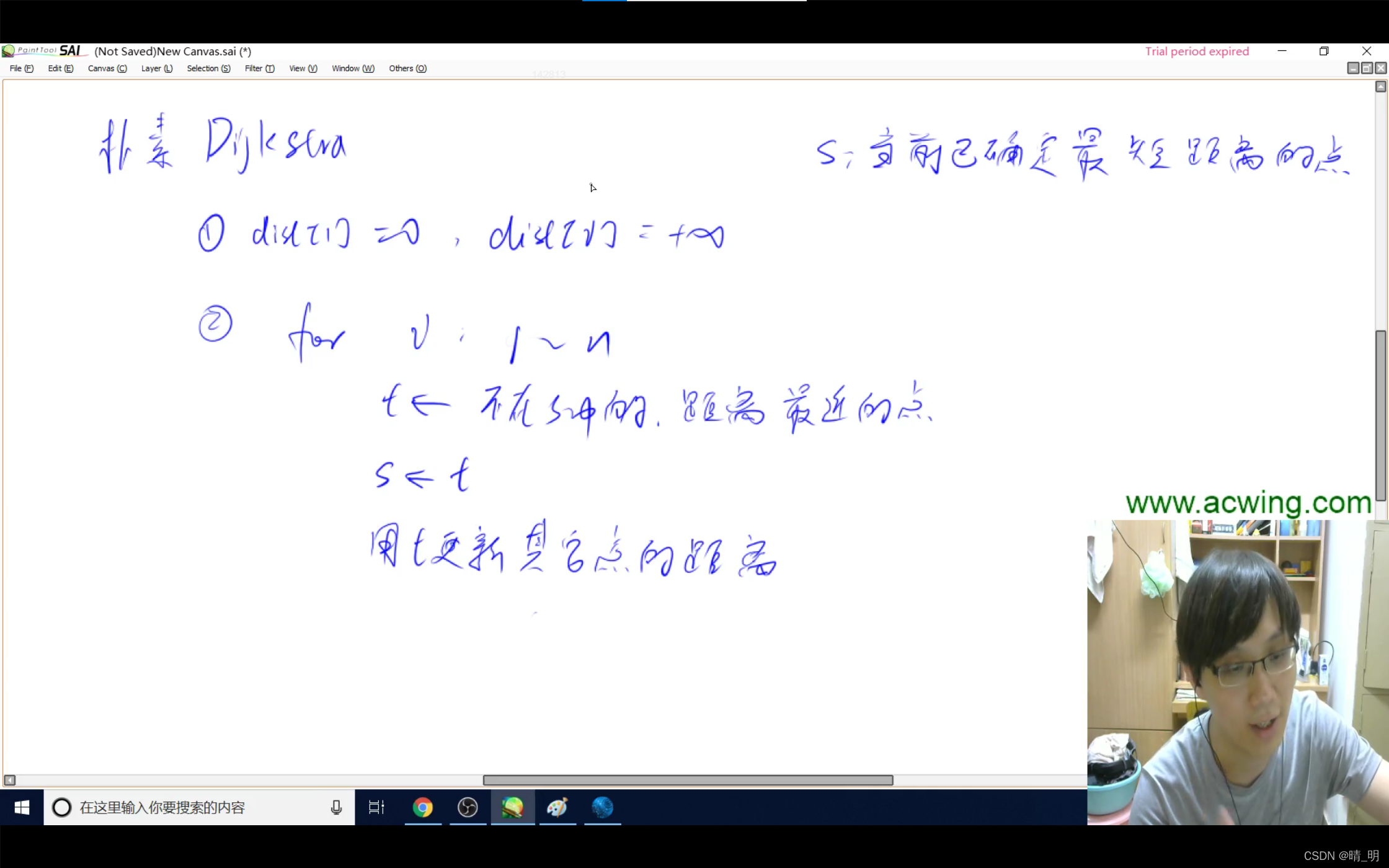
朴素 $Dijkstra$ 算法

模板代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
int g[N][N];  // 邻接矩阵，存储每条边
int dist[N];  // 存储1号点到每个点的最短距离
bool st[N];   // 存储每个点的最短路是否已经确定
 
// 求1号点到n号点的最短路，如果不存在则返回-1
int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
 
    // 先选中一个点，剩余 n - 1 个点，迭代 n - 1 次
    for (int i = 0; i < n - 1; i ++ )
    {
        int t = -1;     // 在还未确定最短路的点中，寻找距离最小的点
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
 
        st[t] = true;
 
        // 用t更新其他点的距离
        for (int j = 1; j <= n; j ++ )
            dist[j] = min(dist[j], dist[t] + g[t][j]);
 
    }
 
    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

个人理解：

$Dijkstra$ 算法严格规定一个点出队即为这个点的最短路，若一个点出队后，之后的点中有负权边，则之前的点应该被更新，但这个点已经出队，无法被更新，所以 $Dijkstra$ 系列算法都无法处理负权边的情况。

具体证明：

  • 如何证明最短路？仅需证明路径中的每一步都为当前的所有可行的道路中的最小值即可，每一步都最小，则所有步相加，必定可以使得结果最小，
  • $Dijkstra$ 算法正是如此，基于贪心的原理，每一次所走的路为当前可走的路中的最小值，所以可以增明最短路，
  • 此外，还可以证明的是当一个点出队时，当前值即为从起点到该点的最短路，思路由数学归纳法可知，和证明终点为最短路类似，令该点为终点，可发现代码实现和原代码如出一辙，由此得证